KS8106 Miller Indicies Molecular Model
Couldn't load pickup availability
Miller Indicies
Miller indices form a notation system in crystallography for planes in crystal (Bravais) lattices. In particular, a family of lattice planes is determined by three integers h, k, and ℓ, the Miller indices. They are written (hkℓ), and denote the family of planes orthogonal to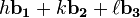 , where
, where  are the basis of the reciprocal lattice vectors. (Note that the plane is not always orthogonal to the linear combination of direct lattice vectors
are the basis of the reciprocal lattice vectors. (Note that the plane is not always orthogonal to the linear combination of direct lattice vectors  because the reciprocal lattice vectors need not be mutually orthogonal.) By convention, negative integers are written with a bar, as in 3 for −3. The integers are usually written in lowest terms, i.e. their greatest common divisor should be 1.
because the reciprocal lattice vectors need not be mutually orthogonal.) By convention, negative integers are written with a bar, as in 3 for −3. The integers are usually written in lowest terms, i.e. their greatest common divisor should be 1. There are also several related notations:
The notation {hkℓ} denotes the set of all planes that are equivalent to (hkℓ) by the symmetry of the lattice.
In the context of crystal directions (not planes), the corresponding notations are:[hkℓ], with square instead of round brackets, denotes a direction in the basis of the direct lattice vectors instead of the reciprocal lattice; and similarly, the notation ⟨hkℓ⟩ denotes the set of all directions that are equivalent to [hkℓ] by symmetry.
Miller indices were introduced in 1839 by the British mineralogist William Hallowes Miller. The method was also historically known as the Millerian system, and the indices as Millerian, although this is now rare. The Miller indices are defined with respect to any choice of unit cell and not only with respect to primitive basis vectors, as is sometimes stated.
There are two equivalent ways to define the meaning of the Miller indices: via a point in the reciprocal lattice, or as the inverse intercepts along the lattice vectors. Both definitions are given below. In either case, one needs to choose the three lattice vectors a1, a2, and a3 that define the unit cell (note that the conventional unit cell may be larger than the primitive cell of the Bravais lattice, as the illustrate). Given these, the three primitive reciprocal lattice vectors are also determined (denoted b1, b2, and b3).
Then, given the three Miller indices h, k, ℓ, (hkℓ) denotes planes orthogonal to the reciprocal lattice vector:

That is, (hkℓ) simply indicates a normal to the planes in the basis of the primitive reciprocal lattice vectors. Because the coordinates are integers, this normal is itself always a reciprocal lattice vector. The requirement of lowest terms means that it is the shortest reciprocal lattice vector in the given direction.
Equivalently, (hkℓ) denotes a plane that intercepts the three points a1/h, a2/k, and a3/ℓ, or some multiple thereof. That is, the Miller indices are proportional to the inverses of the intercepts of the plane, in the basis of the lattice vectors. If one of the indices is zero, it means that the planes do not intersect that axis (the intercept is "at infinity").
Considering only (hkℓ) planes intersecting one or more lattice points (the lattice planes), the perpendicular distance d between adjacent lattice planes is related to the (shortest) reciprocal lattice vector orthogonal to the planes by the formula:  .
.
The related notation [hkℓ] denotes the direction:
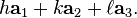
That is, it uses the direct lattice basis instead of the reciprocal lattice
To demonstrate the relationship of Miller Indices to the crystallographic axis of a crystal, please see models KS8105 and KS8106. These models use a simple cubic lattice, 4x3x2 cells, constructed of blue balls except that a (111) plane is shown in.
This model is hand made in the USA by Klinger Educational Products. This is a permanent structure. We only use grade A materials. The 1 inch balls are made of hard Maplewood that includes an enameled painted finish. Polished steel rods are used to connect the wooden balls together.
Miller Indicies contains 112 - 1 inch balls.
















